求道之人，不问寒暑（八）

从2015年开始，《求道之人不问寒暑》这个系列已经写了很多年了，主要聚焦点在深度学习的理论分析上。理论研究虽然很难下手，挫折甚多，但从未停止，一直坚持到了今天，在可见的将来，还会继续坚持下去。

一直以来我是动力学分析的忠实追随者，希望把非线性神经网络的关键训练过程搞清楚，把中间各层的特征如何学习出来搞清楚。只有基于第一性原理的分析，才能真正明白深度学习中出现的各类的实验现象。如果脱离动力学，把神经网络抽象建模成一个能力强大，可以拟合任意函数的黑盒，那对现实世界很难产生实际上的指导作用——因为第一个疑问就无法作答：如果一个可以拟合任意函数的黑盒有如此好的效果，为什么以前的Kernel SVM, Boosting，乃至K近邻都不可以？它们都可以拟合任意函数的。另一方面，如果只用实验现象构造唯象理论，那么往往会得出很多的局部理论，想要把它们糅合在一起，难度往往不亚于从头开始。

当然说的容易，做起来是很难的。从2017年开始，我做监督学习的动力学分析，但一个核心问题是，如何对数据的标注做合理的假设。假设强了，比如说强到线性可分，那整个分析就意义不大；假设弱了，那就很难跳出最差情况（比如说标注随机），这时就只能使用Rademacher Complexity或是VC dimension这种一般化的分析方式，无法用到网络独有的性质。

一个比较折中的假设是学生-教师网络（teacher-student network，见ICML’17, ICLR’18, ICML’18, ICML’20和AIStats’21）。此假设认为数据的标注是从一个教师网络里生成出来的，这样它能自带某种结构，然后我们就可以研究，学生网络是否能通过学习教师网络的输入输出，来学到教师网络的内部结构。然而这样的假设同样存在弱点：即便现实数据的标注来自于某个教师网络，但因为教师网络本身是个黑盒，于是这个假设究竟有多强，什么样的教师网络才可以正确建模现实世界，就不好确定了。

从2020年下半年开始，我开始切换到自监督学习（self-supervised learning）这个大的方向。在这方向上做理论分析还是比较好的。首先自监督方向很新，已有工作不多；其次，所用的目标函数存在某种对称性，有一些漂亮的性质；再次，自监督的预训练过程不涉及标注，这样就无需对此做假设。唯一要额外考虑的是数据增强，不过这个相比之下好处理得多；最后，从自监督的分析里，我们可以看到很多新的性质。

在自监督这个方向上，这次介绍一下，最近我的两篇arXiv在对比学习（contrastive learning）上的进一步工作。

第一篇arXiv文章（Understanding Deep Contrastive Learning via Coordinate-wise Optimization）是关于常用目标函数（loss function）的分析。首先，目前用的很多目标函数，可以写成如下的一般形式：

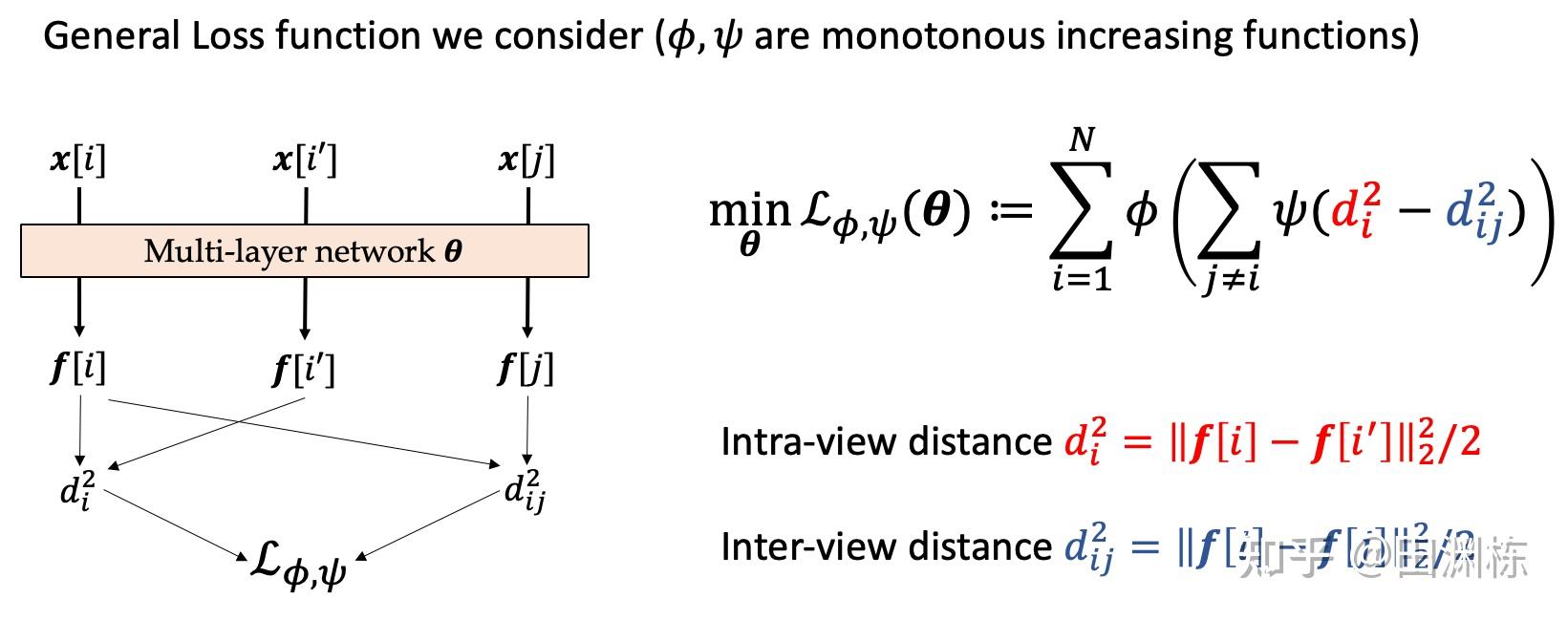
然后，我们证明包括InfoNCE在内的一大类对比学习目标函数，等价于一个有两类变量（或者说两类玩家）参与的交替优化（或者说游戏）过程：

玩家 $\boldsymbol{\theta}$ 负责通过梯度上升找到更好的神经网络参数，而玩家 $\alpha$ 则负责找到当前批次中表示（representation）最相似的两个不同样本，即所谓的hard negative pair，并增加它们的权重。更有意思的是，对于不同的对比学习目标函数，玩家$\boldsymbol{\theta}$ 所要优化的目标函数都是一样的，而玩家 $\alpha$ 的策略各有不同。这样，只要任意修改玩家 $\alpha$ 的策略，就可以等效地产生各种不同的对比学习目标。这个框架，就命名为 $\alpha$ -CL。

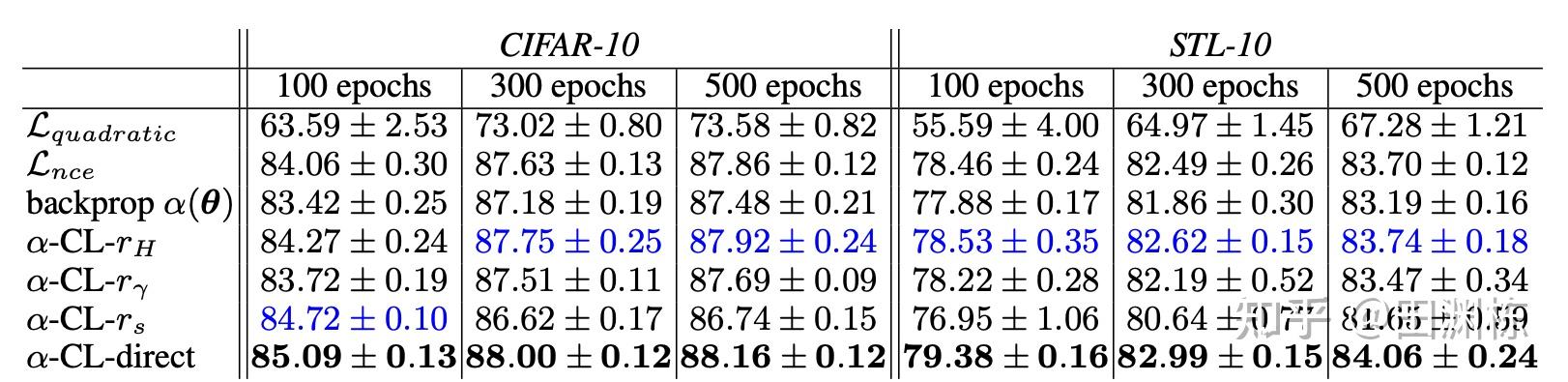
在CIFAR10和STL-10上，文中测试了由这个框架得到的一些简单新算法，都有不错的效果，相信如果挖掘更深，会发现更有效的策略。注意这里我们并不是增加一个外来的优化环节，而是证明目前对比学习优化函数的梯度下降动力学里面，自然存在这样的分工，这样就对目前的方法有更深入的了解。

然后文章中进一步分析了如果玩家 $\alpha$ 固定不动时，玩家 $\boldsymbol{\theta}$ 的行为。一个有趣的结论是，如果网络是多层线性，那么玩家 $\boldsymbol{\theta}$ 的优化结果就是主成分分析（PCA），而且每层最终的权重是秩为1的矩阵。这就建立了对比学习和传统无监督算法之间的联系，同时也暗示了，假设网络为线性的分析结果，并不会超出传统算法的范畴。

那么，对比学习为什么能在各种任务中有远高于线性模型的结果？秘密肯定是藏在多层非线性神经网络里面，是目标函数，网络架构与训练算法三者的结合，才产生了这样一个效果。之前做的线性分析（如ICML’21 Outstanding paper honorable mention, ICLR’22）虽然能揭示一些问题，但它终有局限。

于是，第二篇arXiv文章（Understanding the Role of Nonlinearity in Training Dynamics of Contrastive Learning）就着重于非线性单元在对比学习中的分析，用的是第一篇文章提出的优化框架，看玩家$\alpha$ 固定不动时，玩家 $\boldsymbol{\theta}$ 在非线性网络下的行为。

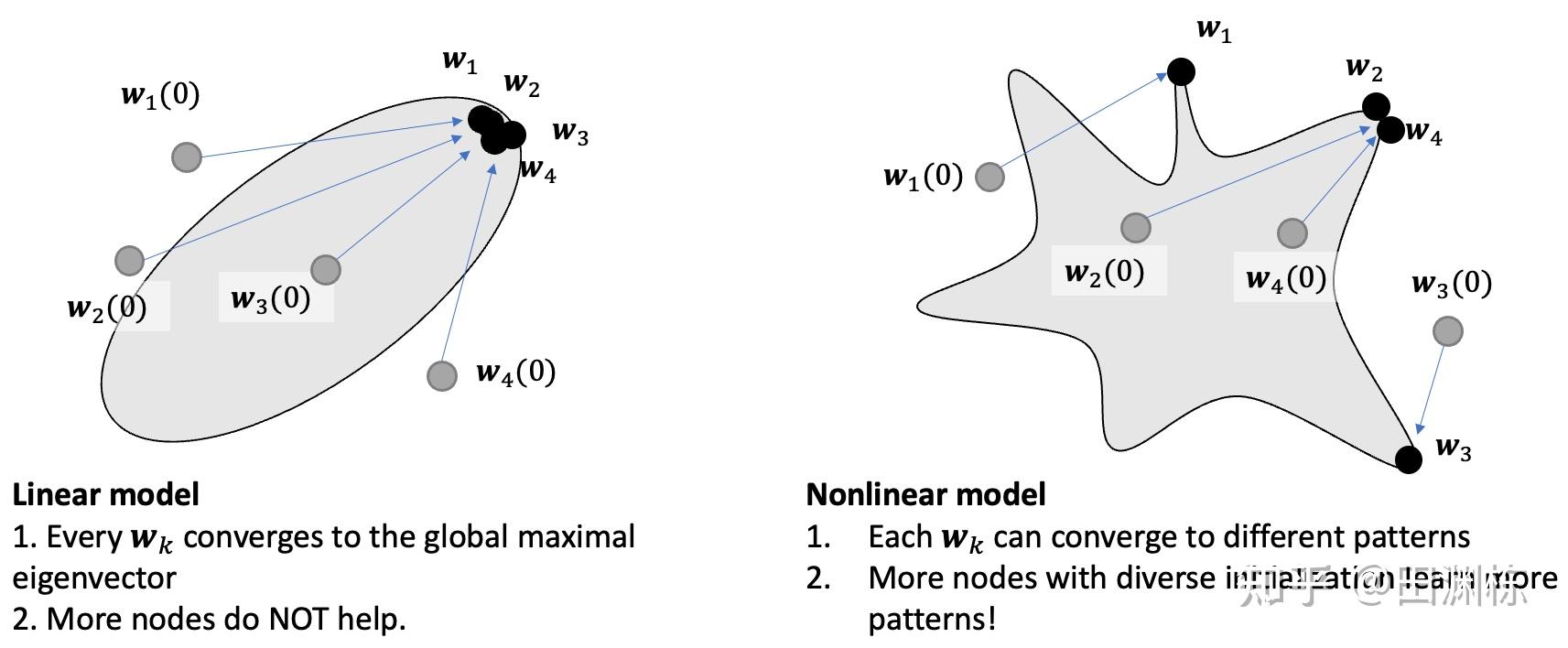
一般来说，非线性的分析，总是从一层及两层网络开始。在单层的情况下，我们可以发现一个有趣的事实：在对比学习下，线性网络的优化因为等同于PCA，只会存在一个主方向，但非线性网络则会存在很多“局部”的主方向，它们是局部的动力学驻点，对应于数据中的多种结构或是模式。

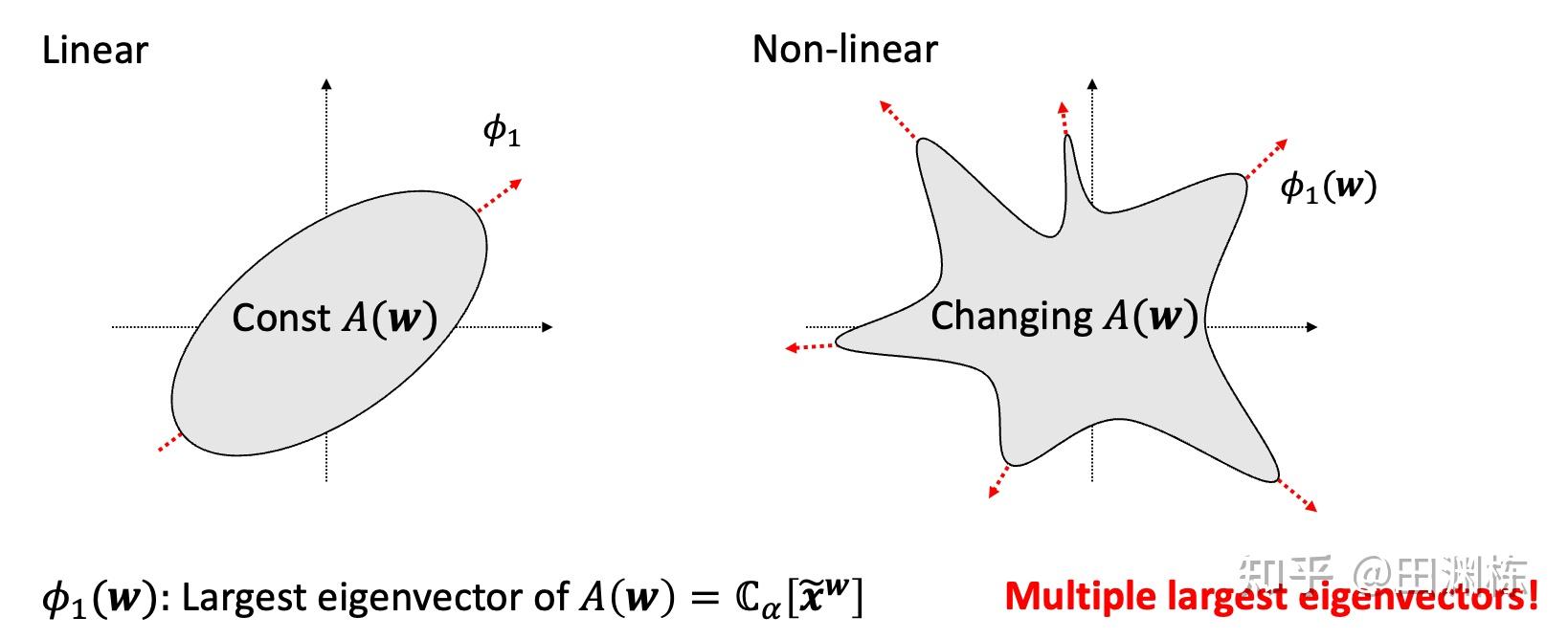
这样的话，非线性网络中经常配备的大量参数就有了意义：只要参数够多，初始化够随机，在收敛完之后，就能尽可能多地覆盖住各种局部主方向，那对应的表示，也就变得更加丰富。这也自然地解释了一些之前观察到的训练现象，比如说彩票假设（lottery ticket hypothesis）。

文章中进一步分析了两层的情况。两层除了有因为非线性引入的大量局部极值点之外，有一个引人注目的机制是全局调制（global modulation）的能力，即上层网络对下层选择性收敛到何种结构的控制力。文章中用多个定理说明了，如果存在一个全局的隐变量 $z$ ，在给定这个隐变量时，输入数据的每个局部感受野（receptive field）相互独立，那么在审视每个局部的学习过程时，就会发现它不仅包括一层网络本来就有的项，还包括从上层传播下来的项，这些项鼓励局部权重学到与全局隐变量高度相关的模式，而不是同等对待局部出现的所有模式。

最后我们做了一些基于生成数据集的对比学习实验，结果与理论分析相当吻合。具体细节可以看文章。

附带说一句，这种上层对下层进行”调制“的思路，其实在我们18年的arXiv上（见Luck Matter）出现过，不过那时因为做的是监督学习，需要对教师网络做一些奇怪的假设，最后技术上实在太难弄得干净，只好放在那里了。可见自监督的数学结构，其实是比较友好的。

总的来说，这两篇文章初步揭示了深度对比学习的一些内在结构。沿着这条路走下去，应当会有更有趣的发现。