求道之人，不问寒暑（六）

好了，ICLR终于结束，而我也有时间再写点东西。

这次介绍一下我们学生-教师网络理论分析的最新进展，这次的工作把它用到了目前比较火的自监督学习（self-supervised learning，缩写为SSL）上，对最近Hinton组提出的SimCLR还有DeepMind提出的BYOL建立了一个理论框架，并且深入多层ReLU神经网络内部，分析出了很多有意思的全新结果，欢迎大家讨论。

【3分钟简介视频】http://yuandong-tian.com/ssl_short.mp4

论文在此：

Understanding Self-supervised Learning with Dual Deep Networks

Yuandong Tian, Lantao Yu, Xinlei Chen, Surya Ganguli

Understanding Self-supervised Learning with Dual Deep Networks首先我们要列一下学生-教师网络的理论分析框架，和最近流行的自监督学习体系如Hinton组的BYOL的相似处和不同点。见下表。

虽然有这么多的不同点，但非常有意思的是，因为两者相似的双塔结构，数学框架是可以从之前的文章里借过来的（见Student Specialization in Deep ReLU Networks With Finite Width and Input Dimension 和之前的求道之人，不问寒暑（五）)。

具体来说，通过对SimCLR+InfoNCE梯度下降的分析，我们找到了一个在多层ReLU神经网络中，每一层权重随梯度更新的关键矩阵，文中称作协方差算子（covariance operator）。

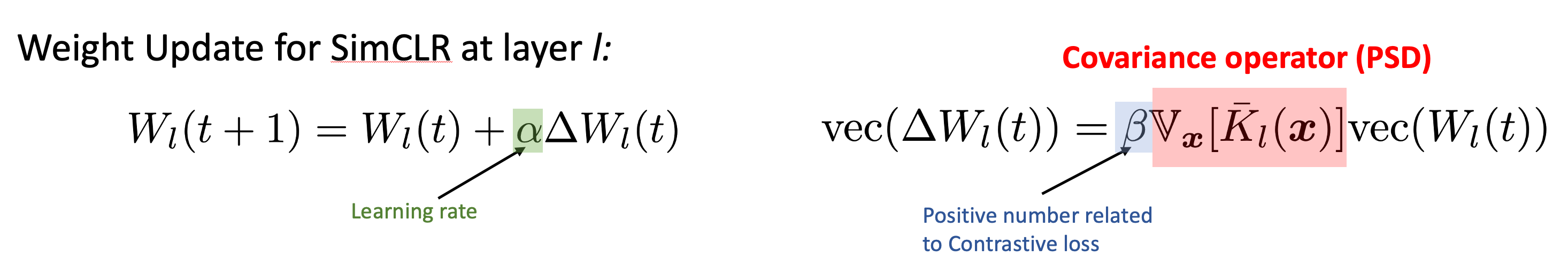
这个算子是随着当前权重的变化而变化的，但在整个训练过程中一直保持半正定。这个结论比较强的地方在于，它不依赖于输入数据的具体分布，也适用于任意的数据增强过程。唯一的假设是InfoNCE这个对比损失函数（contrastive loss）向下传播的梯度是近似常数。如果大家嫌这个假设比较强，那么采用简单的“正样本间距减去负样本间距”作为对比训练的目标函数，这个假设就是简单成立的。

在数学上有这个算子之后，我们看它究竟在训练中起到了什么作用。为此就得要假设数据的生成模型（generative models），和数据增强（Data Augmentation）这个过程，对其造成的影响。 这里的主要想法是数据由两组主要的隐变量生成，$z_0$ 和 $z'$，其中 $z_0$ 和数据的”类标签”相关，在数据增强之后不会发生改变；而 $z'$ 则囊括了生成过程中与类标签正交的部分，比如说图像旋转和缩放程度等，在数据增强之后，$z'$ 会发生变化，见下图：

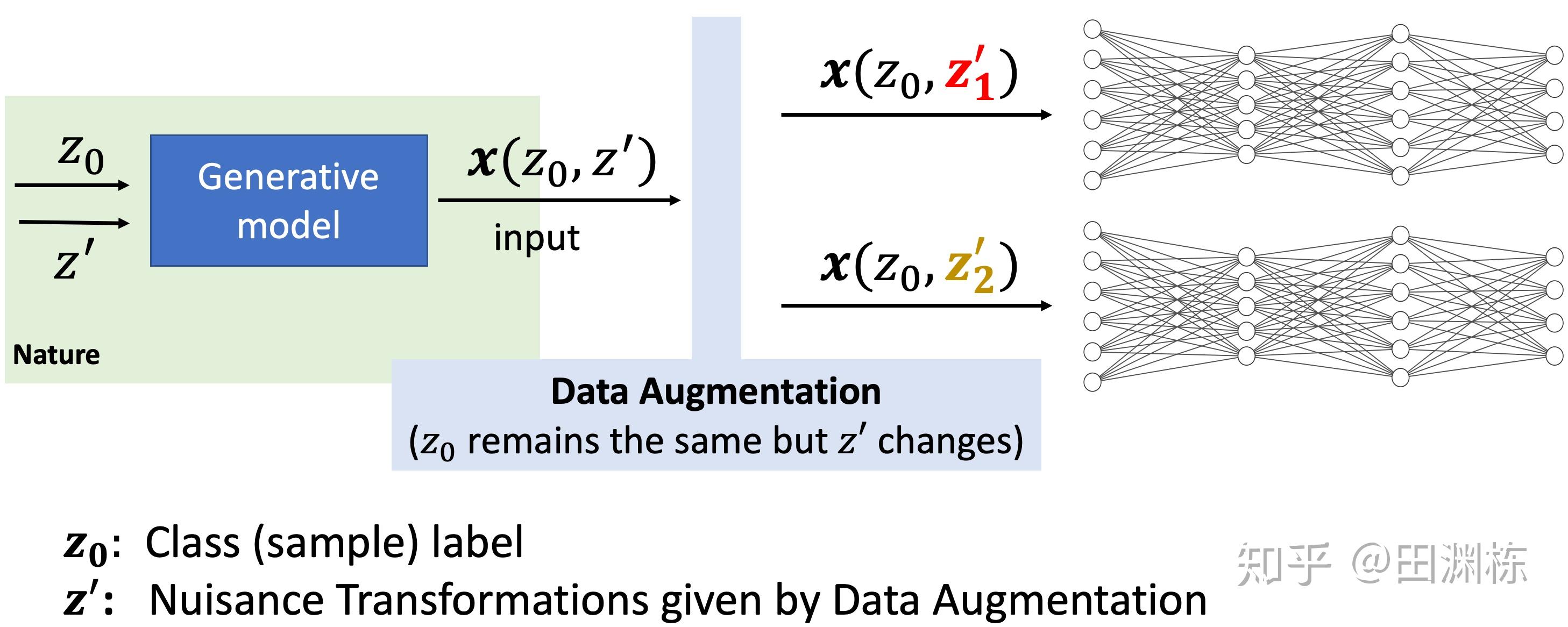
在这个模型下，协方差算子及由它驱动的权重更替，其实就是放大不同类标签的输入数据之间的区别，这种“放大”是通过寻找初始权重中的随机涨落，然后放大对应权重分量来实现。 在不同的生成模型下，协方差算子的行为并不一样。我们主要分析了几种有代表性的情况。 首先当然是最简单的单一神经元的一层网络，和具一维平移不变性的两类物体识别问题，在这种情况下协方差算子有解析解。 但有趣的是，如果神经元是线性的，这个算子是零（所以没有权重更新发生），只有在神经元是ReLU的情况下，才会利用初始涨落学会并且巩固学到的有效特征。这就显示出了神经网络中非线性变换的重要性。

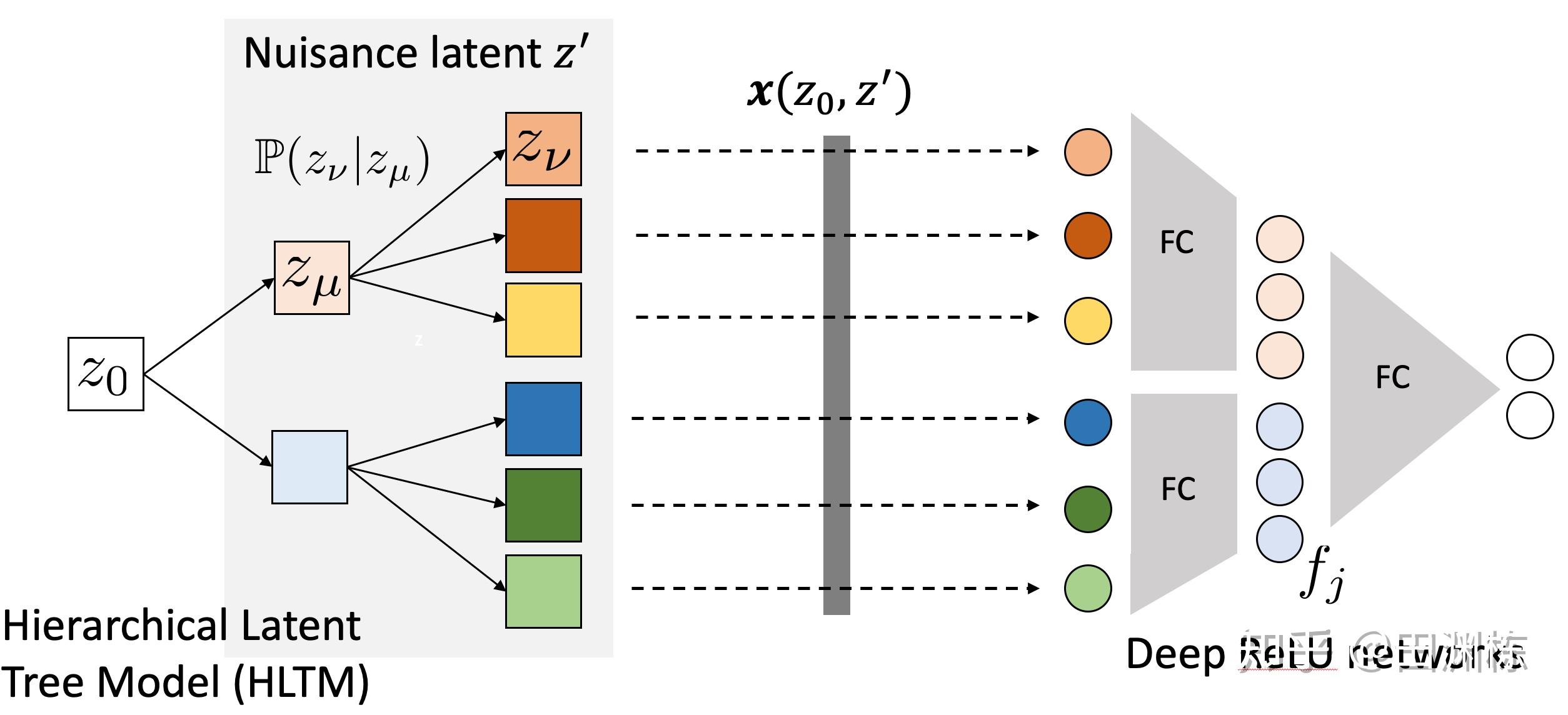
在此之上，我们进一步分析了一些更复杂的情况，比如说两层ReLU的权重同时训练时，上下两层的协方差算子会产生互动，上层的训练成果会改变下层协方差算子，从而加速了下层的权重学习，这就是多层训练的好处。之后，我们还分析了一个更加广义的生成模型，即层次式隐变量树模型（Hierarchical Latent Tree Model, HLTM）与多层受限感受野的ReLU网络的互动，发现有相似的结论，并且还能看出来ReLU中间层的神经元，能学到对应的树模型同层隐变量的值，即便这些中间层在SSL训练时，并没有收到任何相关监督信号，这个就很有意思了，一定程度上揭示了神经网络训练的内部过程。

最后一部分，我们用这个框架来分析最近DeepMind提出并大火的BYOL。BYOL的神秘之处在于它能在没有任何负样本对参与训练的情况下产生效果。这让人非常疑惑，因为如果只有正样本对，神经网络应该偷懒让所有的输出都是常值才对。那它的秘方究竟在哪里呢？

除了没有用负样本对之外，BYOL有三个地方和SimCLR非常不一样，一个是它的双塔结构不是对称的，被训练的那个网络（online network）在头部多了一个predictor；第二个是作为参照的网络（target network）和被训练的网络参数不同，其参数用的是指数移动平均（EMA）；另外最近的一篇文章表明，BYOL需要predictor或者projector里面有BatchNorm（BN）才可以产生效果，而SimCLR有没有BN都无所谓。所以我们就针对这些因素进行了分析。我们先将BN简化成“对前一层的输入作零均值”的操作，这样它对反传梯度的效果，就是对梯度进行零均值：

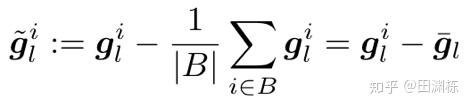
这样反传梯度的值较没有BN时发生了改变，这个改变导致了权重更新的改变。 我们加入一些简化之后可以算出权重更新的公式。

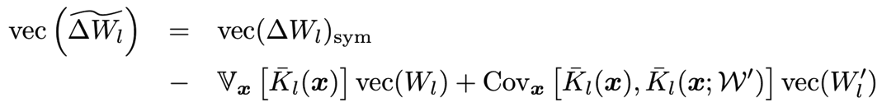
这个公式里面的第一项是鼓励类标签相同的样本其表示也相近，如果只有这项，BYOL应当收敛到平凡解。后两项更有意思，负项是之前提到协方差算子的相反数，而正项则类似协方差算子本身。 有趣的是，因为BYOL的不对称性，负项是个关于predictor的二次项，而正项是个关于predictor的一次项。 如果predictor里面的权重其绝对值比较小，那么负项的幅度要比正项小，正项占主要贡献，于是协方差算子再次登场，而BYOL也就有效。 相比之下，如果是SimCLR的话，因为对称性，这因为BN而多出来的修正项正好是零，所以没有影响。以下一个简单的STL-10的实验表明了反传梯度零均值是重要的：

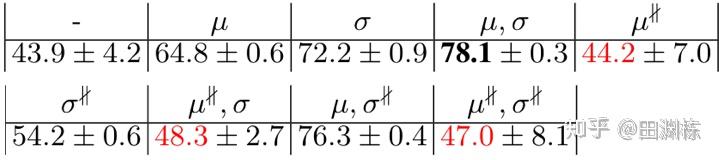
上表中 $\mu$ 表示有零均值，$\mu^\nparallel$ 表示前向零均值但反传梯度不零均值（相当于PyTorch里面x = x.mean(0).detach())，结果发现只要是有 $\mu^\nparallel$，结果一定不好，侧面说明反传梯度零均值的效用。当然这并不表明零均值这个操作是一定必要的（像除到方差为1的标准化操作也有效），更多的分析留待下一步工作。

另外，我们对EMA也做了一些分析，用到了信号与系统中的Z变换来分析这个时间序列。 分析结果表明如果正项比负项稍大，则权重随时间变化会指数增大（也即开始学习）。 虽然指数增长会被最后一层的归一化所遏制，但毕竟不太稳定。 而EMA的平滑功能则能让它能继续学习（极点在单位圆以外），但指数提升的速度不要那么快，这样可以让训练过程变得稍微稳定一些。

文中还有很多实验，大家有兴趣的话可以细看，欢迎讨论。