介绍两篇NeurIPS的文章（二）

本次中稿的第二篇文章是Learning Search Space Partition for Black-box Optimization using Monte Carlo Tree Search (https://arxiv.org/abs/2007.00708)

Linnan Wang, Rodrigo Fonseca, Yuandong Tian

源代码已经公开，欢迎大家使用，一作知乎账号dsakdla

facebookresearch/LaMCTS（我们相关的工作还有一篇叫LaNAS，主要是将这个方法用在神经网络架构搜索（NAS）上，源码也在上面的repo里包含了：Sample-Efficient Neural Architecture Search by Learning Action Space https://arxiv.org/abs/1906.06832。Linnan Wang, Saining Xie, Teng Li, Rodrigo Fonseca, Yuandong Tian）

这篇主要是提出了一种新的黑盒优化（Black-box optimization）的方法。这个新的方法叫LaMCTS (Latent Action Monte Carlo Tree Search)，顾名思义这个是基于蒙特卡罗树搜索（Monte Carlo Tree Search）的，但在这上面有改进。

传统的MCTS的目标是在给定状态空间（state space S）、行动空间（action space A）及状态转移函数（transition matrix, S, A -> S’) 之后，通过搜索找到最优的行动序列，以获得最大的奖励。MCTS搜索是通过增量构建一棵以初始状态 $s_0$ 为根的树来实现的，树中的每个状态结点 $s$ 都有一个简单的模型 $\hat+Q(s,a)$ ，描述如果选择行动 $a$ ，根据过去的经验会有多少奖励。新叶子结点的构建则权衡了过去的经验（exploitation）和探索新的结点（exploration）这两个目标，随着搜索的进行，新叶子会更多集中在有希望的区域里面。

乍一看，MCTS和规划有关，和黑盒优化似乎无关，那它们之间是如何建立联系的呢？

一般来说，黑盒优化都是从一个初始解出发，通过不停迭代来改进当前解，直到无法再改进为止。其主要性能指标是：达到同样的函数值，需要多少次黑盒函数的调用，越少越好。因为在实际问题中，需要用黑盒优化的场景，往往是函数调用开销非常大且没有导数信息的场景，比如说函数值是一个复杂系统运转一天后的平均效率，或者是耗费巨资才可获得的一个实验结果，等等。

这个黑盒优化的迭代过程可以用各种方案去刻划：比如说从一个还不错的起始点开始的局部搜索，一个从粗到细的逐步精化，或者说局部渐进和长程跳跃的组合（例如进化算法的演化和突变），等等，每种方案都对应不同的行动空间。但从本质上来说，优化和“下棋打游戏”等问题很大的不同点在于，优化本身没有”行动空间“的概念，对它而言，行动空间如何定义都无所谓，只要最终解质量好就行。

与其使用各种人工定义，**自然的想法就是学一个行动空间出来。**这就是这一系列文章的贡献。

我们以“解空间的切分”作为广义上的行动空间，而具体的切分方式，则是在每个MCTS的树结点上，用过去获得的样本点学一个最好的切分函数出来——我们希望这个切分函数能将好的和差的样本点尽量分开，这样一刀切下去，如果能将质量差的解空间统统切掉，以后少分配些搜索资源，那就是最理想的了。而MCTS兼顾exploitation和exploration的特性，使得即便一开始切得不够好，以后也有扳回来重新划分空间的余地。而每个叶节点的空间，就是它的所有祖先节点的切分的交集。

以下是一个神经网络架构搜索（NAS）上的简单例子。假设我们要搜索一个一至五层的卷积网络，每层的filter数是32或是64，filter大小可以是3x3或者5x5。考虑两个不同的行动空间，一个是逐层确定每层的参数(filter数及filter大小)，另一个是先确定网络层数，再确定每层的参数。从图上可以看到，明显是先确定网络层数的方案效率更高（同样样本下准确率更高），因为相对其它参数，层数对最后网络准确率的影响更大，如果先按层数切分搜索空间，那搜索效率自然就提高了。

洞察到了这些问题之后，我们提出了LaNAS和LaMCTS。LaNAS采用线性函数切分空间，对于叶节点的函数值估计则采用简单的随机采样法，及最近比较流行的one-shot supernet。LaMCTS做了改进，采用非线性函数切分空间，并且在叶节点上用了已有的黑盒优化的方法比如说Bayesian Optimization（BO）来找到叶节点的子区域里的最优解。

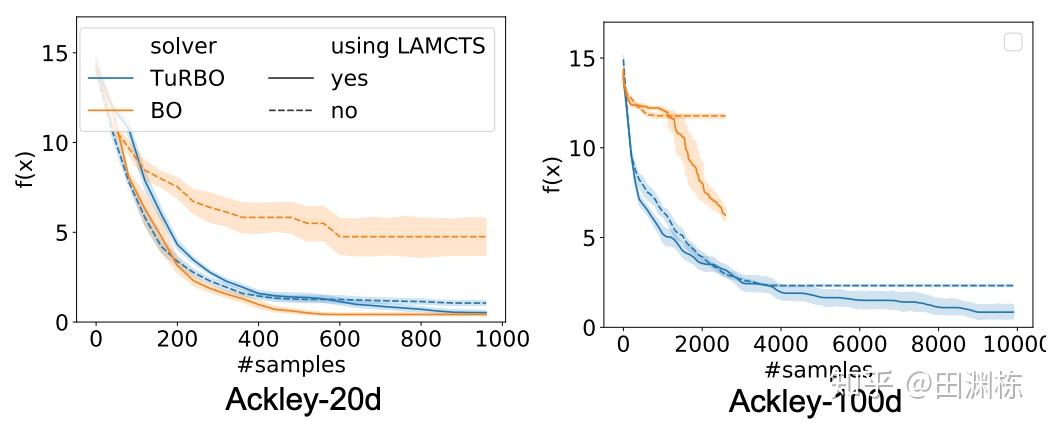
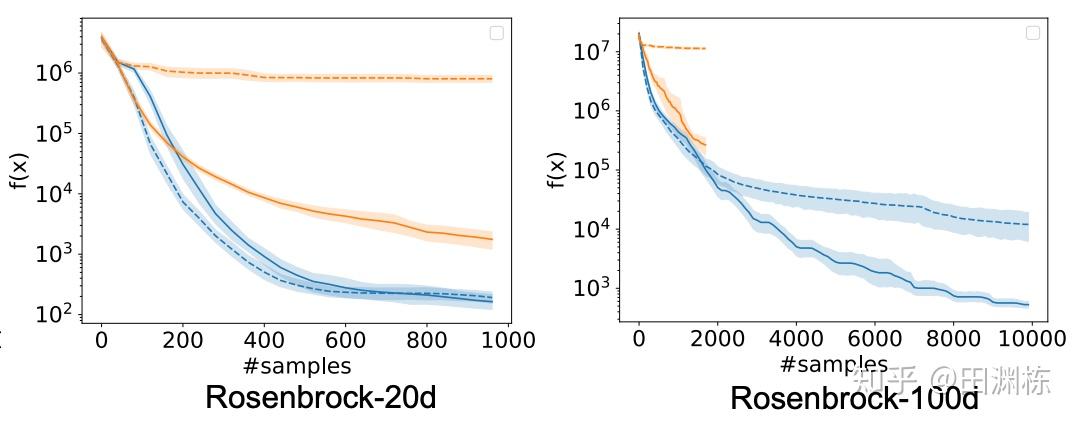
通过这个方式，特别对于高维问题达到同样性能，我们发现LaMCTS可以达到更低的样本复杂度。这里我们在Mujoco的任务上做了测试，和各种已有的黑盒算法进行了比较，蓝线是我们的方法：

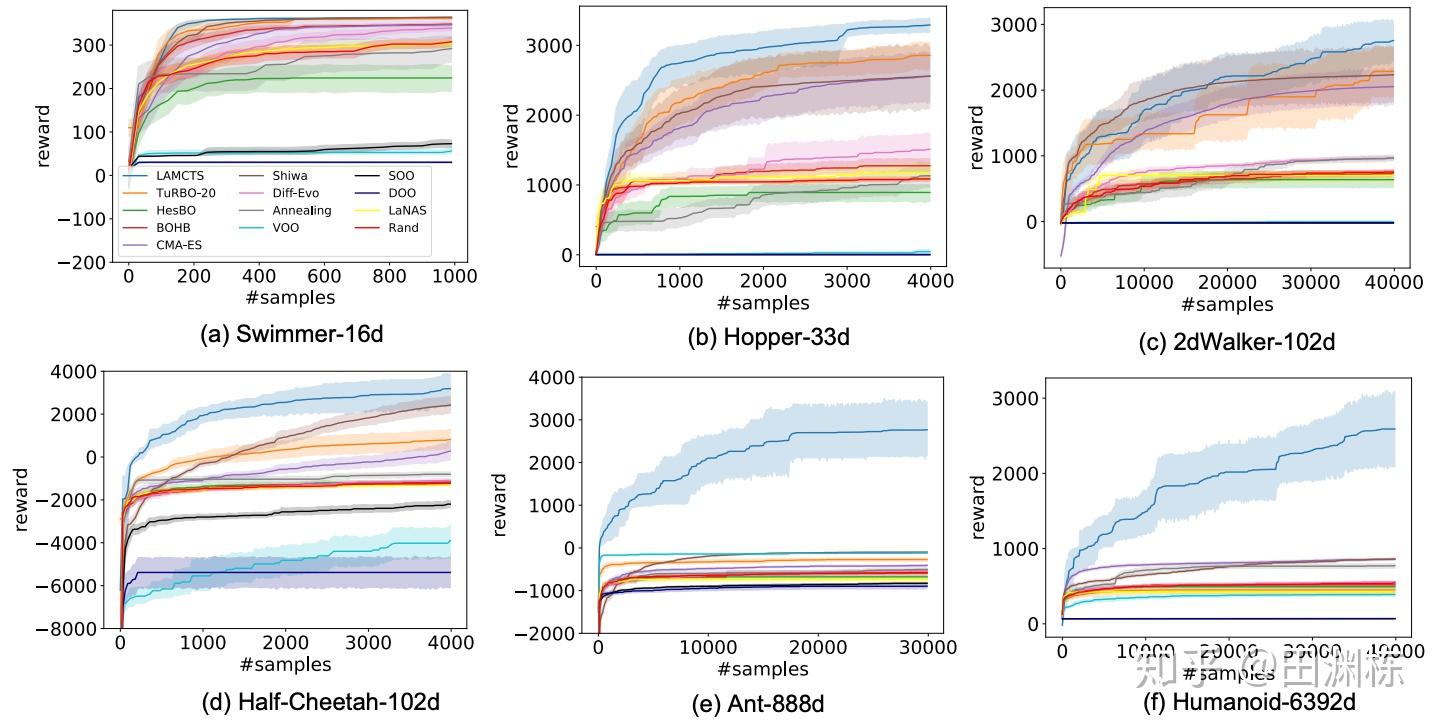
当然LaMCTS和基于梯度的方法相比，在Mujoco的高维问题上还是有差距（因为Mujoco其实并不需要太多探索）。我们指出了自身的局限性，出乎意料地被reviewers们交口称赞。

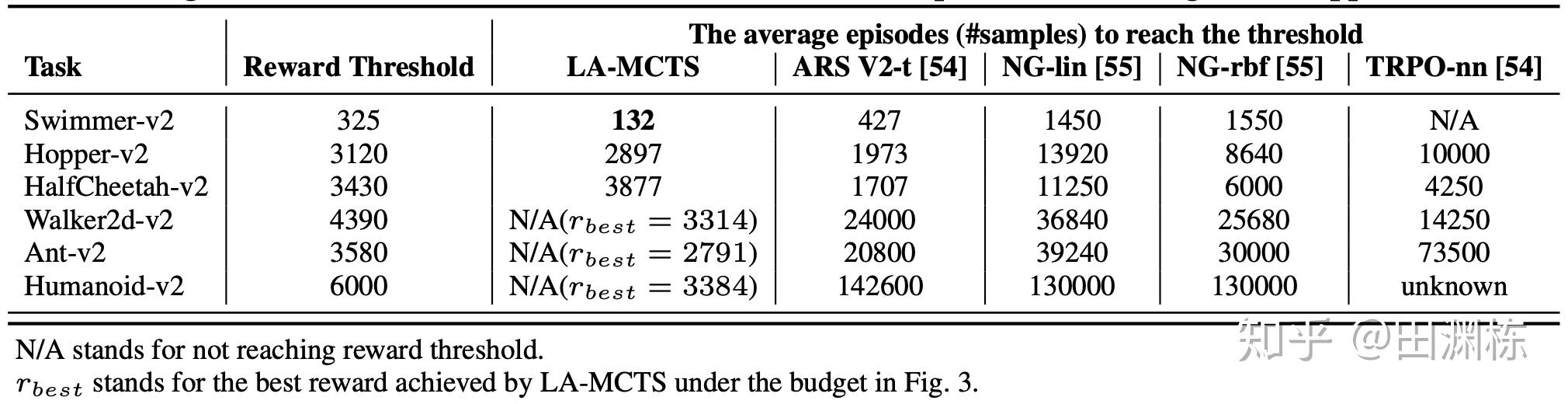
因为每个叶结点采用了已有算法，LaMCTS也可以套在任何已知的黑盒优化算法上，作为一个元算法（meta-algorithm），让整个系统达到更好的效果。为什么能提高呢？主要原因是，传统方法像Bayesian Optimization (BO）在参数空间维数很大（比如上百维）的情况下，由于维数灾难的问题，高斯过程（GP）的建模效率就会大打折扣。而LaMCTS通过切分空间，让GP的建模局限在一个比较小的范围内，从而提高了它的效率。