今天NeurIPS 2020放榜,我这里中了两篇主打文章,乘着周五大家还关注NeurIPS的情况,且我们内部ICLR的deadline已过,写两篇小博客各自介绍一下。
Joint Policy Search for Multi-agent Collaboration with Imperfect Information (https://arxiv.org/abs/2008.06495) Yuandong Tian, Qucheng Gong, Tina Jiang
这篇文章设计了一个新的算法,来试图解决多智能体合作时联合优化策略的问题。对于不完美信息两人零和游戏(比如说两人德州扑克),用现用的一些算法(比如说CFR)可以在理论上保证当迭代次数足够时一定收敛到纳什均衡点。但不完美信息多智能体合作的策略优化则要困难很多,并且往往会陷入局部极小值。
比如说有两个玩家合作,玩家A抽一张暗牌0或1,然后向玩家B发一个0或1或2的信号,让玩家B猜A手上的牌是什么,猜中得1分,猜不中则得0分。显然在这种情况下,存在 种协议,这6种协议是完全对称的,采用任何一种玩家B都可以猜中得1分。但如果规则稍微改一下,比如说发送1有0.1的附加分,那若A和B采用“抽0发0, 抽1发2”的协议,就赚不到这个附加分,是局部极小策略。但A和B单方面都不想改变自己的策略,因为单方面改变的结果是对方不理解自己策略的改变,导致得分的下降。
那在这种情况下,要如何去优化各自的策略呢?很多策略优化方案采用就是按坐标优化(Coordinate Descent),即假设其它人的策略不变,然后优化自身的策略。这显然在这里不太可行。而同时优化多个智能体的策略,在不完美信息的条件下,又是比较困难的,见下图:
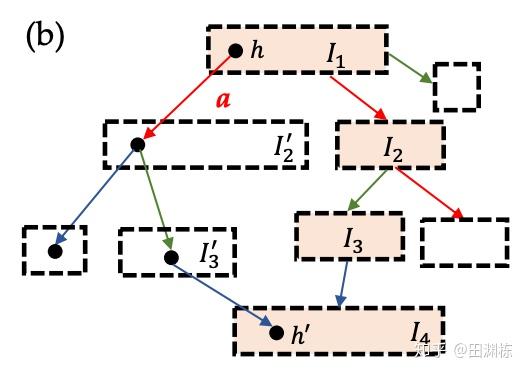
假设带阴影的这些信息集(Information Set)上的策略需要优化,但问题在于如果改变了上游的策略,则下游信息集内各状态的可到达概率就会发生各种变化,从而隐含地改变下游的期望得分;而下游策略的改变,又会改变上游的期望得分。这就使得策略与收益得分相互间的影响变得非常复杂,而且存在“牵一发而动全身”的关系,让联合优化变得非常困难——如果我们只想修改1000个信息集中的3个信息集的策略,那其它997个信息集上的期望得分也会发生变化,即便它们之上的策略并没有发生任何改变。
这篇文章的一个主要贡献,就是找到了一个”策略变化密度“(policy-change density)这样一个量,满足以下两个条件:(1) 不管上下游的策略是否发生了变化,如果一个状态的当前策略没有变化,那策略变化密度就为0,(2)策略变化密度在所有状态上的总和,就是整个游戏得分因策略变化后的改变量。
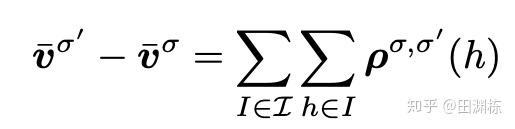
有了这个公式之后,再要联合优化策略就变得相对容易了。这篇文章采用的是简单的深度优先搜索,从上游策略出发,先改变上游策略,然后给定上游策略,再改变下游策略,如此往复,然后看最后整个游戏的得分改变量的大小,最终选出最好的新策略组合。这样就能达到联合策略搜索(Joint Policy Search)的目的,并且这样的算法得到的策略性能一定是单调上升的。
运用这个方法,我们先在一些小规模的非完美信息合作游戏(主要是桥牌叫牌阶段的简化版)上进行了测试。我们从CFR得到的联合策略开始,用搜索算法对当前的联合策略进行改进(CFR1k+JPS),直到陷入局部极大值为止。结果发现确实有用,新的策略都改进了得分,而且越复杂的游戏,改进越大(这部分代码已经开源,请见这里)
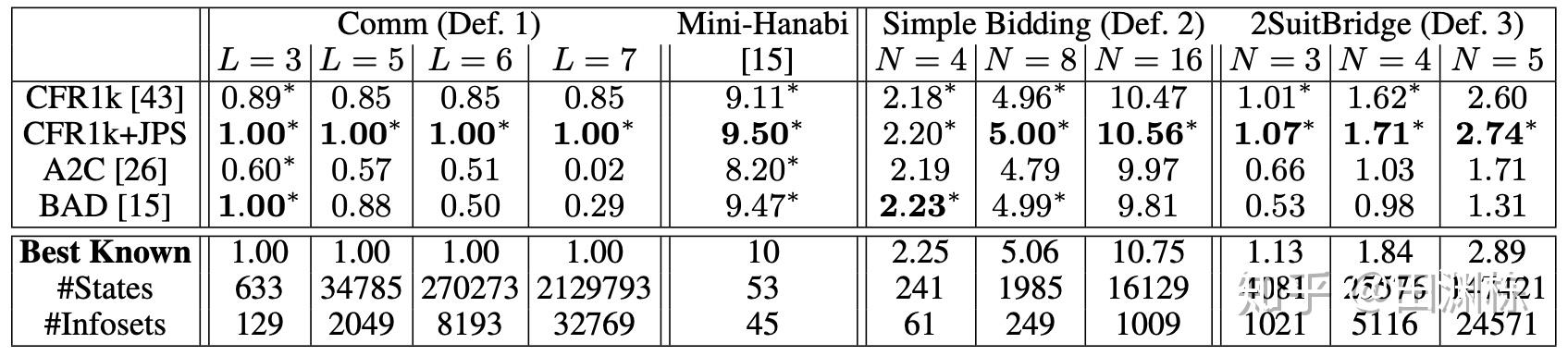
最后当然是在真的桥牌叫牌环境下进行测试。我们先用A2C自对弈训练了一个还不错的基线策略,然后用上文提到的联合策略搜索(JPS)来改进队友间的叫牌约定,并且和目前较好的桥牌AI软件(WBridge5)进行了一千局开闭室比赛。比赛是JPS和JPS一队,WBridge5和WBridge5一队。最后发现和基线策略相比,我们的效果确实变好了。注意这里的两阶段训练没有用到任何人类对局,为的是能够无监督地学到全新的叫牌约定——让机器学到人类所不知道的新东西永远是很有意思的。
当然这里有个问题是我们只做了叫牌,没有做打牌,叫牌完了之后游戏就结束了,并以双明手(double-dummy)的分数,即所有牌摊开来打,来定胜负。WBridge5是以正常叫牌加打牌的模式来优化的,并且事先也没有领教过我们学出来的新叫牌约定,所以这个比较不是特别公平(也被reviewer们使劲狂喷),但目前只有这个办法(这部分代码暂不开源,因为各种小trick比较多,之后等全部搞完了再说)。

IMPs/b (平均每桌的国际比赛分)这个应该算是目前最好的结果了(State-of-the-Art)。