求道之人，不问寒暑（七）

好了，乘着今年NeurIPS的截稿日推迟了48小时的机会，抽空介绍一下今年ICML中稿的文章。

这次有幸中了三篇Long talk（每篇long talk约3%的中稿率），算是运气爆棚，感谢给力的合作者们！这里先讲一下我的一篇获得Long talk的一作文章Understanding self-supervised Learning Dynamics without Contrastive Pairs，其它两篇之后再讲。

最近在理论方面，以之前的学生-教师网络分析为基础，这边的研究方向渐渐转向分析“表示学习”（representation learning）的训练原理。这篇文章就是针对最近出现的一些新型的，无负例样本对的表示学习算法（如BYOL和SimSiam），进行了一些梯度下降动力学上的分析。

在自监督学习（self-supervised learning）中，对比学习（contrastive learning）是一个非常通用的学习方案：虽然没有样本标注，但我们可以假设数据增强（data augmentation）永远将一个样本转换成和它同类的样本，然后要求通过数据增强的样本，其输出的表示（representation）和原样本的representation尽量保持接近；而不同的样本，也即是负例样本对，其representation则尽量不同。这样学得的representation，自然能对数据增强造成的样本变化具有鲁棒性。

如果说对比学习的原理大家还是能理解的话，那无负例样本对（non-contrastive）的学习算法就相当神奇了：我们可以把负例样本对去掉，只对由同一样本生成的两个正例样本对进行训练，算法居然还能学出一个有意义的表示。

看到这个现象，大家自然会觉得，为什么学习算法不会找到偷懒的秘方，收敛到一个常值表示的平凡解呢（称为崩溃Collapsing）？这样的话，正例样本对的要求自然满足，因为它们输出的表示永远是相同的。

一开始大家觉得可能是BatchNorm的问题，BatchNorm的归一化让同一个batch里面的不同样本之间成了自然的负例样本对，为此我们去年的文章（见）对此做了一些分析，不过在两周之后旋即被DM的人反驳，他们拿出实验结果证明就算没有BN，BYOL的训练也是能成立的——所以这也许并不是本质原因。

我们这篇文章于是对此进行了更深入的分析——先从最简单的线性架构开始。

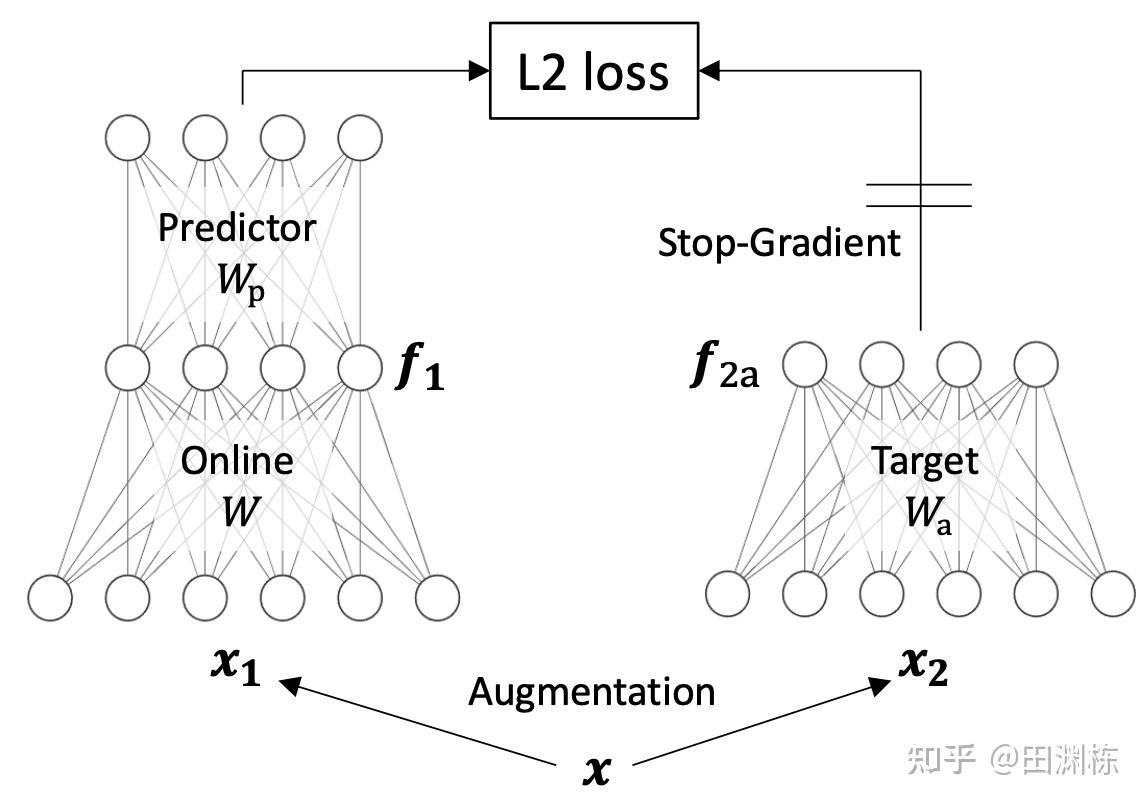
以上是一个最简单的non-contrastive self-supervised learning的架构。两边都是线性的，一边多一层预测器（predictor），另一边的梯度不能反传（stop-gradient）。之前的文章（包括鑫磊和恺明的SimSiam）都通过实验证明了，这两个附加的结构，对于学习算法不崩溃至关重要，但理论上这是怎么回事呢？

很有意思的是，我们这篇文章通过分析这样一个最简单的线性架构，就可以产生很多理论上的推断，并且这些推断都与实验事实吻合。首先，我们可以写下这个系统的目标函数和动力学方程：

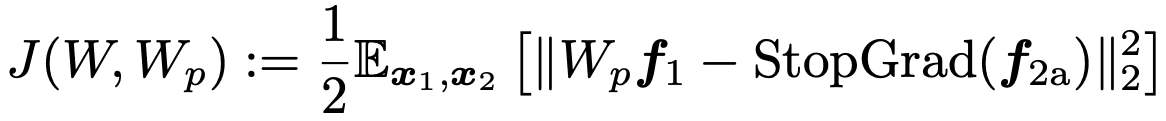
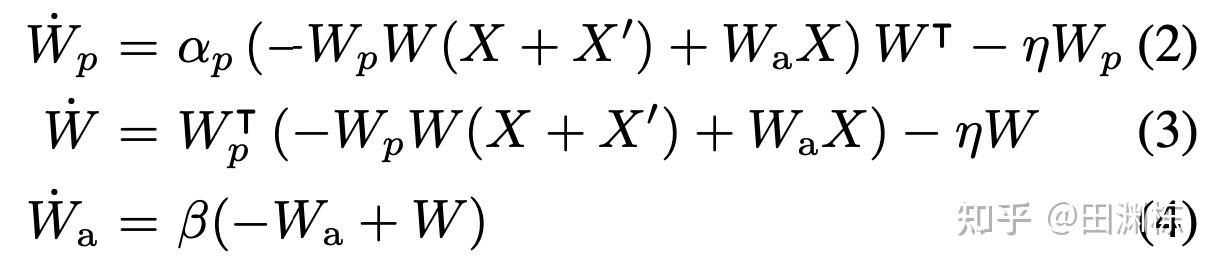
注意到这个动力学方程里有三个超参数， $\alpha_p$ 是预测器（predictor）的学习率， $\eta$ 是权重衰减率（weight decay）， $\beta$ 是指数衰减移动平均（Exponential Moving Average）的速率。这篇文章的一个主要贡献，就是通过理论分析预测出这三者对学习过程和结果的影响。

给定这个模型，经过一些简单分析，我们可以立即发现如果没有“梯度不能反传”的条件，那这个动力学方程会立即让权重W收敛到平凡解。在理论上，我们就能直接计算到了以前的文章的实验结论：

更有趣的是，这个理论分析的一个关键部分（文中定理3）是发现了在训练过程中， 预测器$W_p$ 和预测器输入的相关矩阵 $F+=+W\mathbb{E}[xx^T]W^T$ 这两者的特征空间会逐渐地趋向对齐（eigenspace alignment），这也被实验所充分证明：

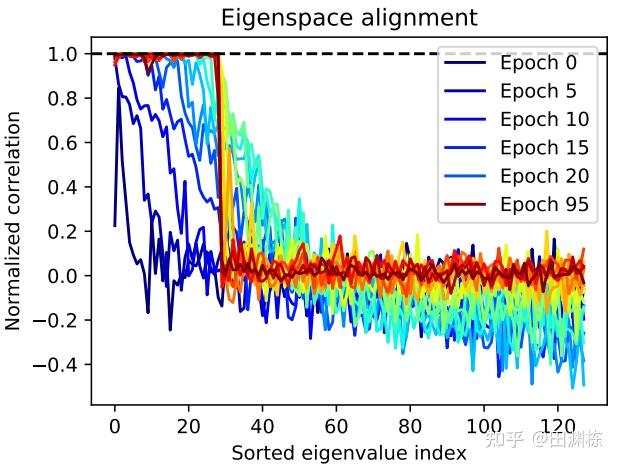
在理论上我们可以证明这个对齐在满足一定条件下是会出现的（这里假设预测器 $W_p$ 是对称矩阵，注意到F也对称，两个实对称矩阵乘积可交换当且仅当它们有相同的的特征空间）：

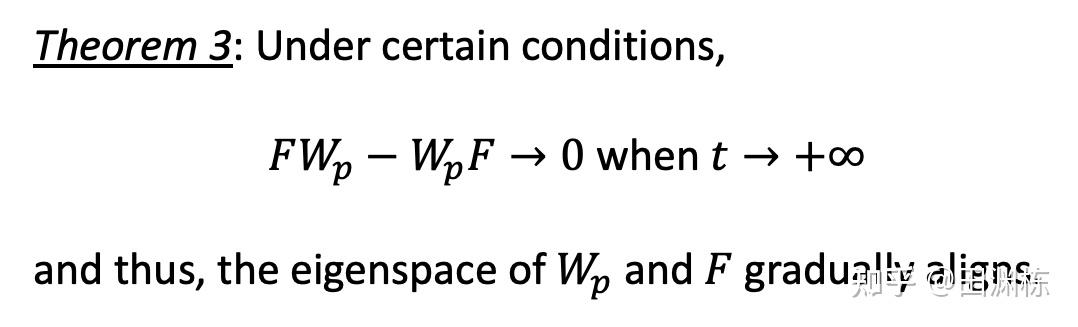
有了这个对齐的条件，整个动力学方程就可以解耦成如下的一维问题，这为接下来的分析提供了极大的便利。式中 $p_j$ 和 $s_j$ 对应于预测器 $W_p$ 和 $F$ 的特征向量，而 $\tau+\le+1$ 则对应于EMA（细节见文章）：

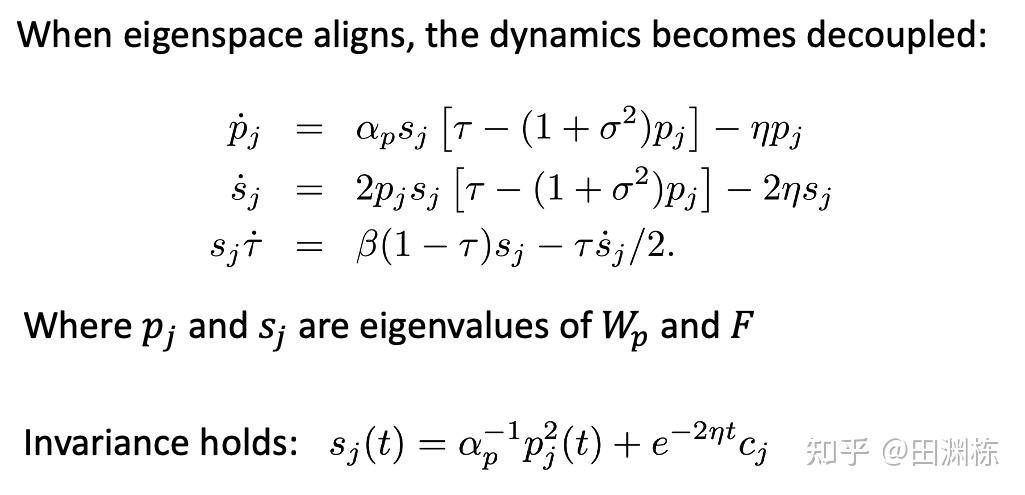
针对这个一维问题我们可以进行大量的细致分析，比如说我们可以发现$W_p$ 的特征值有好几个稳定解。其中零点是平凡解，但还有一个非零的非平凡解，BYOL类的算法在训练时为什么能不崩溃，为什么可以收敛到好的表示，都是因为有这个非平凡解的存在。

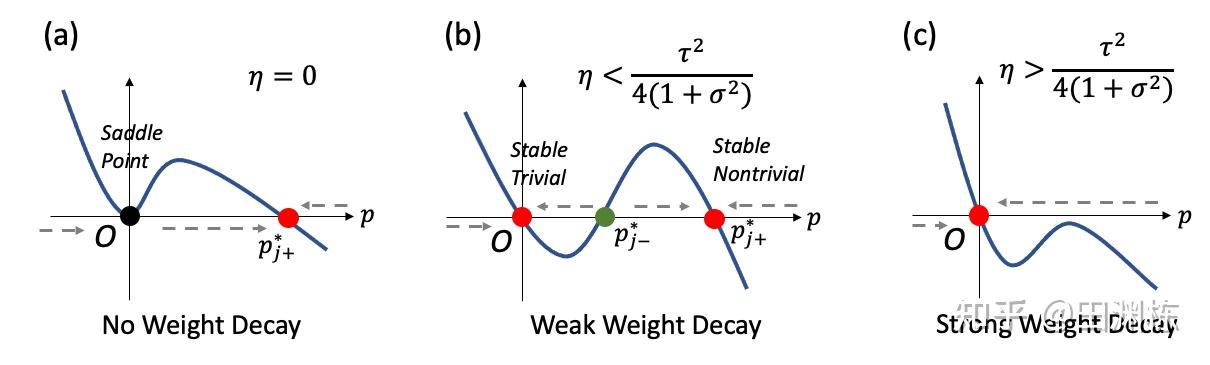
另外，从解耦的方程来看， 所谓“预测器”$W_p$ 其实是一个优化函数动力学上的“缓冲”，通过同时和下方的网络参数（以 $F$ 为代表）一起增长，来驱动下方网络的学习过程，让其能进行下去。如果没有 $W_p$ ，或者说$W_p$ 一开始就是单位阵（ $p_j=1$ ），那么这个动力学只会得出 $\dot+s_j+<+0$ ，从而压制 $F$ 的特征值 $s_j$ 让它趋于0，不会增长，那么学习也不会进行。

使用这解耦的方程，我们对这个动力学方程的三个超参数 $\alpha_p$ （预测器学习率）， $\eta$ （权重衰减率）还有 $\beta$ （指数衰减移动平均的速率）进行了细致分析，列出了10条具体的现象（见下表），并且用大量的实验表明这个分析和实际实验相当一致。

注意我们在做实验的时候，用的是多层的非线性神经网络（ResNet18），训练样本也是CIFAR-10和STL-10，所以和分析用的线性模型并不一致，但令人惊奇的是，理论预测的趋势和实验仍然符合得很不错。具体的细节我就不在这里讲了，大家可以看文章。

从我们的分析之中，又会冒出一个自然的想法：如果梯度下降的最终目标是让这两者的特征空间对齐，那为什么不修改训练算法，让它们一开始就对齐呢？文章的后半段就设计了一个新算法叫DirectPred。根据相关矩阵F的估计，在训练时直接计算出预测器$W_p$ 的值，看看学习效果如何：

结果正如我们所料，在对算法进行了这样一顿大改之后，新的学习算法照样可以学会好的表示，并且比用梯度下降优化线性预测器的效果更好：

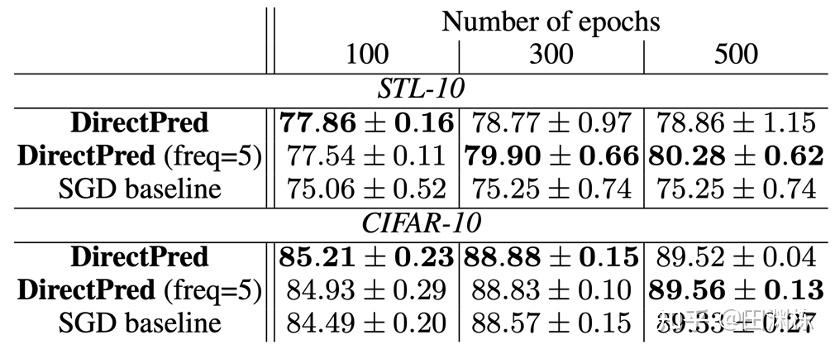
在ImageNet（60 epochs）上也有相似的结果。DirectPred效果好于线性predictor，与使用两层的predictor的效果相当（Camera Ready之后这张表更新了，增加了300 epoch的结果，与原始的BYOL结果一致，在Top-5上甚至还有0.2%的小提升，感谢鑫磊！）：

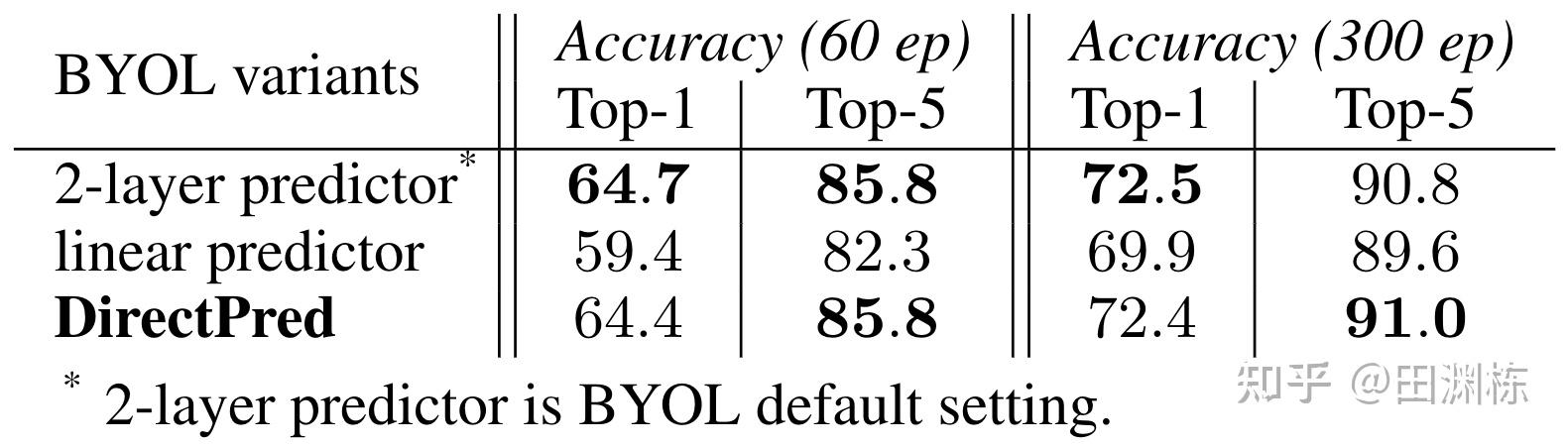
以后如果能拓展完成两层predictor的理论分析，或许会得到更好的算法出来。不过数学上可能会相当复杂，留待之后再处理了。

总的来说，这篇文章算是比较幸运的理论和实验相当吻合的例子，做完之后也非常高兴。所有五个评审都给出了一致的好评，最后的分数是4Accept + 1Strong Accept，没有悬念地中了。在做完了CIFAR-10和STL-10的实验之后，在ImageNet用同样的思路直接就有效果，而没有通过使劲堆机器疯狂试验，这是很不错的了，当然这也亏得鑫磊在ImageNet上一流的实验功底，非常感谢！